Our research project is centered around the notion of randomness in quantum theory. There are three main ways in which probabilistic phenomena appear in quantum mechanics:
- as models for typical quantum states and operations, usually described by random matrices
- intrinsically, as the results of quantum measurements and their effects on quantum systems
- as noise, providing stochastic models for environments interacting with quantum systems.
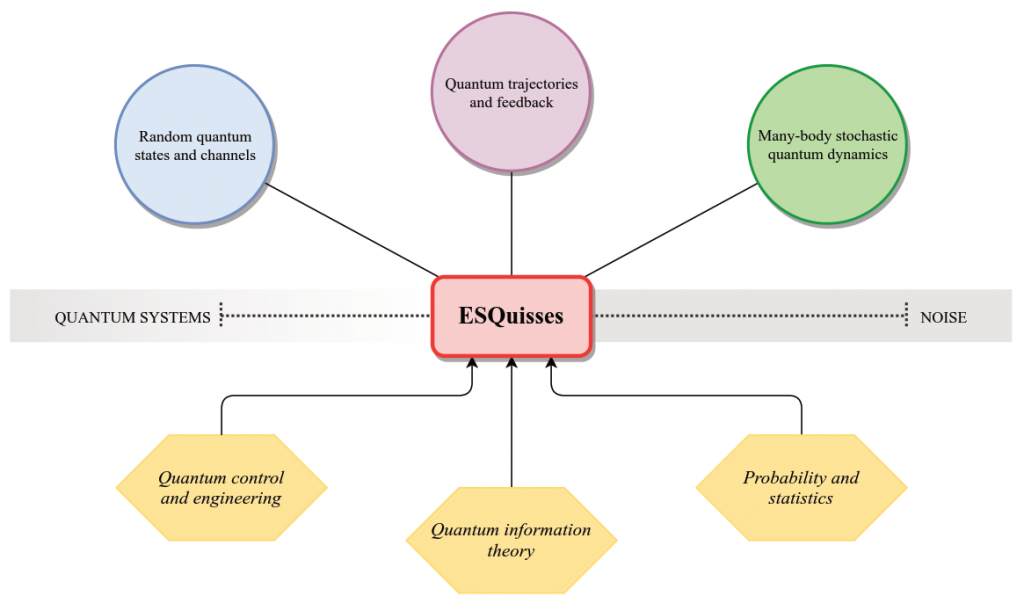
These three manifestations of stochastic processes in quantum theory are strongly interconnected. Our proposal is grounded on synergies between the members of our consortium having different areas of expertise and approaches to studying these problems. More precisely, we shall focus on three main topics, each pertaining to one of the categories above: random quantum states and channels, quantum trajectories and feedback, and many-body stochastic quantum dynamics. The theoretical insights gained on stochastic quantum evolutions will be key to current challenges in quantum physics, such as observable distributions in random quantum circuits and channels, obtaining information from indirect measurements with and without feedback, controlling or correcting noisy quantum systems, taming information or entanglement propagation and transport in many-body systems, etc.
Work packages
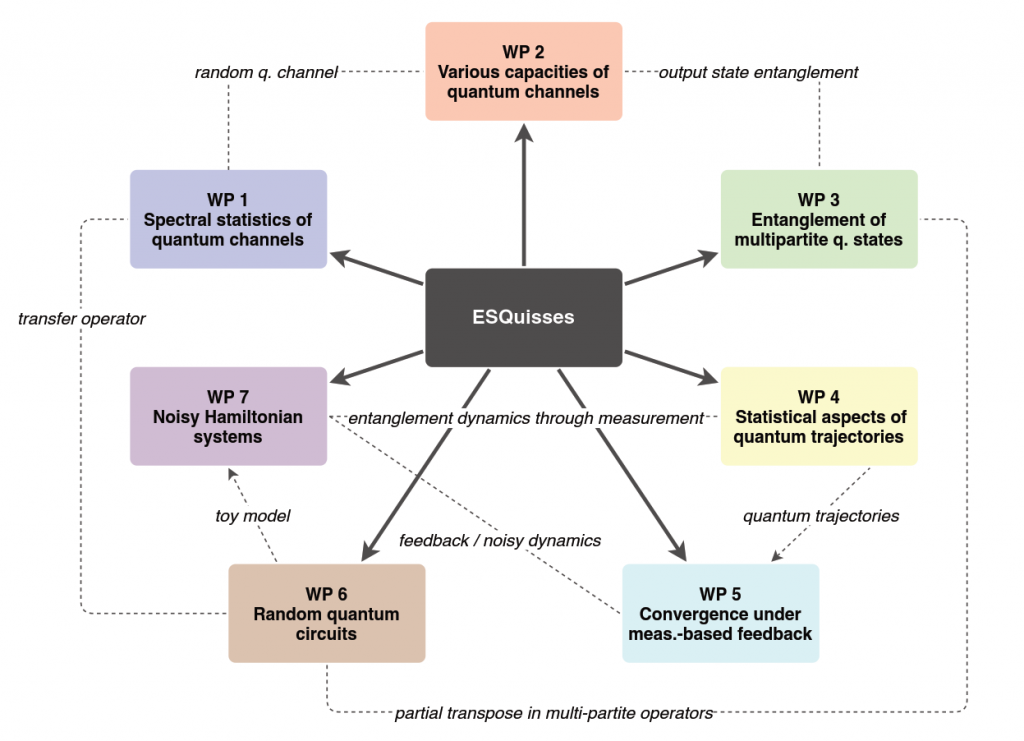
A. Random quantum states and channels
WP1: Spectral statistics of quantum channels
Task 1.1: Rigorous results for the spectral gap of random quantum channels
Task 1.2: Correlation length of random matrix product states
WP2: Various capacities of quantum channels
Task 2.1: Additive bounds for entropic quantities
Task 2.2: Characterization of the output set of tensor products generic quantum channels
WP3: Entanglement of multipartite quantum states
Task 3.1: Multi-partite entanglement via tensor norms
Quantum trajectories and feedback
WP4: Statistical aspects of quantum trajectories
Task 4.1: Estimation of the measurement efficiency parameter
Task 4.2: Estimation of the interaction parameters
WP5: Convergence and robustness under measurement-based feedback
Task 5.1: Simple output feedback scheme stabilizing a target subspace
Task 5.2: Quantum-state feedback scheme stabilizing a target subspace
C. Many-body stochastic quantum dynamics
WP6: Random quantum circuits
Task 6.1: Rigorous results for random quantum circuits
Task 6.2: Perfect tensors and dual unitary quantum circuits
WP7: Noisy Hamiltonian systems
Task 7.1: Exact solution to Quantum Symmetric Simple Exclusion Process and applications
Task 7.2: Exact solution to Quantum Asymmetric Simple Exclusion Process and applications